食塩水の公式は3つ覚えればOK？苦手な問題の攻略と考え方を解説

中学受験に出てくる食塩水の問題は難問が多く、苦手なお子さんも多いでしょう。似たような紛らわしい食塩水の公式が覚えられず、ますますやる気を失う場合もあるかもしれません。

算数は掛け算まではわかっても、割り算や割合（％）が出てきて分からなくなる場合が多いですね。この記事では食塩水の濃度を計算する公式や、裏ワザなどをご紹介します。

食塩水の公式を覚える前に

食塩水の濃度の問題は小学校5年で習う割合の勉強の時や、中学で習う一次方程式、連立方程式と理科の水溶液でも出て来ます。

 

中学受験では割合の計算問題として出題されることが多いようです。食塩水の濃度の問題は中学でも苦手とするお子さんが多いので、小学校のうちに解き方を理解しておけば中学に入ってからの学習も容易になりますね。

 

ではまず食塩水の問題の解き方を見る前に、食塩水にはどんな性質があるのかを見ていきましょう。

食塩水は【食塩と水】

食塩水は「食塩と水」から出来ています。食塩は水に溶かしたからと言って無くなってしまうわけではなく、水の中に存在しているのです。

 

その証拠に食塩水をどんどん熱していって水を蒸発させると、溶かしたはずの食塩が姿を現します。目に見えないくらいの小さい姿になっていただけで、食塩は水の中にいたわけですね。

 

つまり、食塩水の重さは以下のようになります。

計算するときに水の重さだけを足して、食塩の重さを忘れてしまうことがあるので要注意ですよ。

量が変わっても濃度は変わらない

食塩水の問題でお子さんが陥りやすい考え方が、「食塩水の量が減ったら濃度も薄くなるのではないか」ということです。食塩水が半分になれば塩の量が半分になるから、薄くなると言った考え方だと思います。

 

食塩水が半分になったら塩の量も半分になりますが、水の量も同じように半分になるので濃度は変わりません。

 

例えば100％のジュースが200gあった時、100gずつ2つのコップに分けても100％のジュースのままですね。濃度は分けても足しても同じ濃度同士なら、変化しないのです。

食塩水の濃度には限界がある

食塩水の濃度は何％まで濃くできると思いますか？100％以上の食塩水はあるのでしょうか？食塩水は食塩と水でしたので、100％の食塩水はつまり「食塩100％」で水は含まれないことになります。

 

理論上は99.9999…％までは食塩水と言えますが、実際は水には決まった量の食塩しか溶けません。実験してみたところ水の温度によって多少の違いはあるものの、濃度約26％程度で食塩は溶けずに下にそのまま沈むようになります。

 

これを「飽和食塩水」といいます。もう食塩をどれだけ足しても、溶けることのない限界の濃度です。ちなみに海水の濃度は約3.5％と言われていますので、飽和食塩水はかなりしょっぱい味がするでしょうね。

食塩水の公式を覚えよう

食塩水の濃度の問題を解く前提は「食塩水は食塩＋水」と「食塩水の量が変わっても濃度は変わらない」の2つです。

 

そんなこと当然と思うかもしれませんが、意外とお子さんはこの前提が理解できていないことが多いのです。もしうまく問題が解けていないようなら、前提条件を理解しているかどうか確認してみましょう。

 

ここからは食塩水の濃度に関する3つの公式と、公式を覚えなくても問題を解けるような裏ワザ的な考え方をご紹介します。

食塩水の3つの公式

食塩水の問題で出てくる用語は以下の3つです。

様々な問題が出題されると思いますが、結局は上の3つのどれかの数字を求めてきます。それぞれの数字を求めるための公式を覚えれば、食塩水の問題は解決したようなものです。

 

3つのそれぞれの数値を求めるための公式は、以下の3つになります。

と思った人も多いと思います。似たような紛らわしい公式ですね。これをすぐに覚えられる人は覚えてしまえば楽ですが、何かもっと別な方法は無いのでしょうか。

公式を【みはじ】で考えてみよう

食塩水の濃度の公式はたった3つですが、似たような紛らわしい公式で覚えるのは大変です。そこで裏ワザとして考え出されたのが、いわゆる「みはじ」「はじき」と言われるT字を使った覚え方です。

 

それぞれ「み（道のり）は（速さ）じ（時間）」「は（速さ）じ（時間）き（距離）」で、速さの問題を解くときに使う方法です。これを食塩水の濃度の計算に応用しています。

 

みはじの関係を現した図は以下の通りになります。

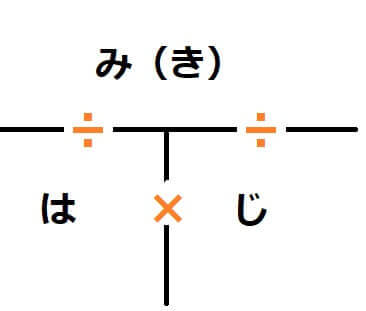
これを食塩水の濃度に当てはめると以下の通りになります。

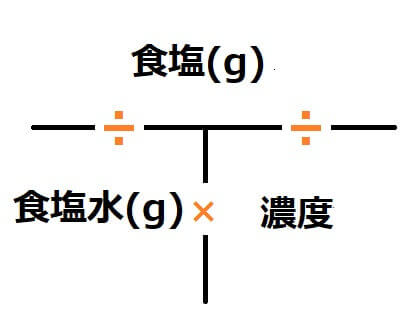
ここで注意が必要なのは、「濃度は％ではなく小数になること」です。濃度が5％なら「0.05」で、濃度が20％なら「0.2」になります。小数に100をかけるとパーセントにできますよ。では使い方を見ていきましょう。

 

図の中で知りたいものを指で隠します。すると2つが残るので、横並びなら掛け算、縦並びなら割り算で計算すると指で隠した部分の数字が出てきます。

 

たとえば5％の食塩水が200gあり食塩の重さを知りたければ、食塩を隠すと「食塩水×濃度」になるので「200g×0.05＝10g」で、答えは「10ｇ」となります。

面積図での考え方

面積図…。筆者は学生の頃こんなものを習った覚えが全くありません。ほとんどの大人は筆者と同じではないでしょうか。

 

中学受験に出てくる食塩水の濃度の問題は難問が多いため、中学受験の対策としてどこかの賢い塾の先生が考え出したのではないかと思います。面積図を使う場合も濃度は％ではなく、小数で考えていきます。

 

考え方としては

・食塩の重さ（g）=食塩水の重さ（g）×濃度（小数）

と、長方形の面積の求め方

・長方形の面積＝たて×横

が同じ計算方法で求められるために、覚えやすい長方形の面積の公式を食塩水の濃度の公式に当てはめてしまおうというのでしょう。基本の面積図は以下の通りです。

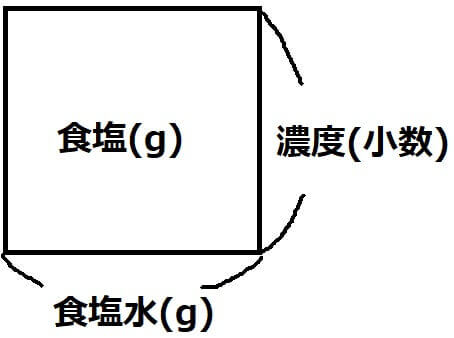
横が食塩水の重さで、たてが濃度を小数にしたものです。面積が食塩の重さになります。さてここからが本題。複雑な食塩水の難問を解く場合は2つの面積図を組み合わせて使います。

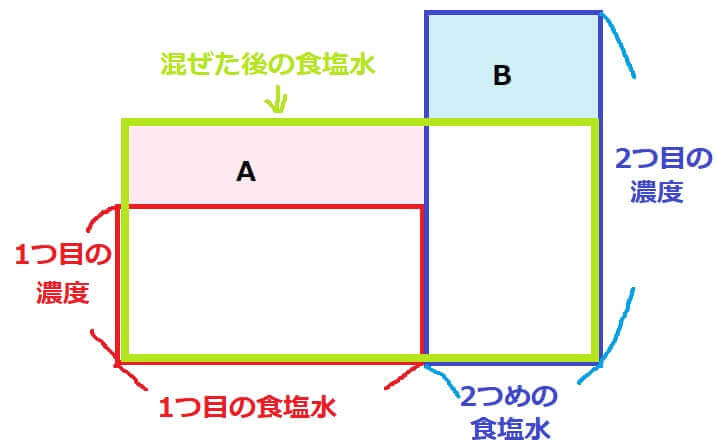
うわー急に複雑になりましたね、ここで一番大事なことは「AとBの面積の値が同じになる」です。どうしてそうなるのかを考えると複雑になるので、単純に「そうなるんだな」と覚えてください。

 

あとは問題文を見て数字をそれぞれの場所に当てはめていけば、計算できますね。後の方で具体的な解き方を説明します。

公式を忘れたら？

難問を解くのは特別な方法を使わないとできませんが、簡単な問題なら解ける筆者の独自の方法を紹介します。これは塾の先生などには鼻で笑われるかもしれませんが、裏ワザの裏ワザとして参考にしてください。

 

筆者は濃度の問題を考えるとき、「100g当たりではどうかな」と考えています。つまり「100ｇの食塩水の濃度と食塩の重さは一致する」という考え方です。

 

5％の100gの食塩水には食塩は5g含まれます。同じように100gの食塩水の濃度が10％なら10g、15％なら15gです。

 

例えば、5％の食塩水400gに含まれる食塩の量を求める問題の場合は、100ｇのコップに入った5％の食塩水が4杯あると考えれば、5g×4杯で、答えは20ｇです。暗算で出来ますね。

 

もう1つ例題、食塩水300ｇに含まれる食塩が6gの時の濃度を求める問題なら、これも100gずつ3つのコップに分けてみると、1つのコップに含まれる食塩の量は6÷3＝2gです。100g当たりの食塩の重さと濃度は一致するので、2％が答えになります。

 

あくまで簡単な問題だけに使える緊急避難的な考え方ですので、試験の時に「あれ？濃度の公式ってどうだったっけ？」となった時などに使ってみてください。

食塩水の公式を使った小学生の問題

食塩水の濃度の問題は、複雑で頭が痛いですね。大人が頭を抱えるものを小学生が解くのですから、中学受験恐るべしです。

今のお子さんは大変ですね、筆者が子供の時は何も考えずに遊びまわっていたことを考えると申し訳ないような気がします。

 

とはいえ受験問題として出題されるなら、解き方を覚えなければいけません。ここからは実際に食塩水の濃度の例題を解きながら、公式や「みはじ」「面積図」の使い方を見ていきましょう。

【例題1】濃度を求める問題

まずは簡単な問題から解いていきましょう。濃度を求める問題です。

【解き方】

この問題で一番間違えやすいのが、全体の食塩水の量の計算です。「食塩水の重さ＝水の重さ＋食塩の重さ」ですので、これさえ間違えなければ解くのは簡単ですよ。今回の問題の場合、食塩水の重さは270ｇではなくて270＋30＝300ｇになります。

 

「みはじ」の考え方で計算すると、濃度は食塩の重さ（30ｇ）÷食塩水の重さ（300ｇ）になります。答えは0.1で、これをパーセントに直すと10％になります。小数をパーセントに直すには、100をかけるのでしたね。

 

答え：10％

【例題2】水を加える計算

例題1はちょっと簡単すぎたかもしれませんね。次は食塩水に水を加える問題です。水を加える問題には濃度を求める場合と、全体の食塩水の重さを求める場合と2種類があります。

【解き方】

これも「食塩水の重さ＝水の重さ＋食塩の重さ」が理解できていれば簡単です。この問題で大切なのは、まず食塩の重さがどれだけあるのかを計算しておくことです。

 

「みはじ」の考え方で食塩の重さを計算しましょう。食塩の重さは「食塩水の重さ×濃度（小数）」なので、400ｇ×0.12＝48ｇで、最初の食塩水には48ｇの食塩が溶けていることがわかります。

 

ここに水を200ｇ加えるので、食塩水全体の重さは400ｇ＋200ｇ＝600ｇですね。水を加えても食塩の量は変わらないので、600ｇの食塩水に48ｇの食塩が溶けていることになります。

 

もう一度みはじを使って、濃度を計算しましょう。濃度は食塩の重さ÷食塩水の重さなので、「48ｇ÷600ｇ＝0.08」です。0.08をパーセントに直すと8％になります。

 

答え：8％

【例題3】食塩を加える問題

次々と解いていきましょう。3問目は食塩水に食塩を加える問題です。濃度を求めることが多いと思います。

【解き方】

濃度の問題の解き方で共通しているのは「食塩水に含まれる食塩の重さをはっきりさせておくこと」です。それがわかっていれば迷うことは少ないでしょう。

 

まず1％の食塩水400ｇに含まれる食塩の重さを計算します。みはじの考え方で、食塩の重さは「食塩水の重さ×濃度（小数）」なので、400ｇ×0.01＝4ｇです。

 

ここに40ｇの食塩を加えるので、全体の食塩の重さは4ｇ＋40ｇ＝44ｇになります。

 

400ｇの食塩水に40ｇの食塩を足したので、全体の食塩水の重さは400ｇ＋40ｇ＝440ｇです。食塩の重さは44ｇなので、濃度は44ｇ÷440ｇ＝0.1になり、小数をパーセントに直すと10％が求める答えになります。

 

答え：10％

【例題4】2つの食塩水を混ぜる問題

ここからはだんだん難しくなってきます。濃度の違う食塩水を、2種類混ぜた時の値を求める問題です。これもゆっくり考えていけば必ず解けますので、あきらめずにがんばりましょう。

【解き方】

濃度を求める問題は必ず食塩の重さをはっきりさせるのが大事です。5％の食塩水200ｇに含まれる食塩の重さは、みはじの考え方から200ｇ×0.05＝10ｇとなります。同じように10％の食塩水300ｇに含まれる食塩の量は300ｇ×0.1＝30ｇです。

 

全部を混ぜるので、全体の食塩の重さは10ｇ＋30ｇ＝40ｇです。また、食塩水の全体の重さは200ｇ＋300ｇ＝500ｇになります。

 

40ｇの食塩が溶けた500ｇの食塩水の濃度は40ｇ÷500ｇ＝0.08です。0.08をパーセントにすると8％になります。

 

答え：8％

【例題5】難問！答えが2つあるなら面積図を使おう

中学受験の食塩水の問題には、答えを2つ求めるものがあるそうです。連立方程式を使えばわけなく解けるのですが、小学校では連立方程式を勉強していないので使えません。

 

そこで登場したのが「面積図」を使った問題の解き方です。意味を考えていくとかなり難解になってしまうので、「こうすれば解ける」やりかたをとりあえず覚えてしまいましょう。

【解き方】

ではまず、やみくもに面積図を描いていきましょう。図の寸法は適当で大丈夫です。そこに分かっている数字をどんどん書き込んでおきます。横は食塩水の重さ、たては濃度（小数）、面積が食塩の重さです。

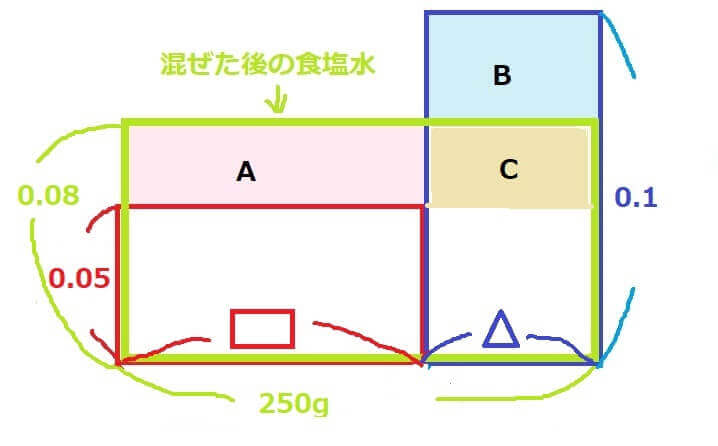
5％の食塩水は赤、10％の食塩水は青、混ぜ合わせた食塩水が緑色の長方形で表されています。

ここでのポイントは2つの食塩水を足したものが緑色の長方形なので、「ピンク色に色を付けたAの部分と水色に色を付けたBの部分の面積は同じになる」ということです。

 

どうしてそうなるのか分からない場合は、「取りあえずそうなっているんだな」と思っていただければ大丈夫です。AとBの面積が同じことだけ覚えてください。

 

AとBの面積が同じなら、「A+C」と「B+C」も同じ面積になりますね。A＋Cの面積は計算で出せそうです。横は250ｇで、たては0.08-0.05＝0.03ですので、A＋Cの面積は250×0.03＝7.5ｇです。

 

A＋Cの面積が分かればB+Cの面積も計算できそうです。この場合たては青い数字の0.1から赤い数字の0.05を引くとB＋Cのたての長さが求められますので、0.1-0.05＝0.05です。横は分からないので、とりあえず「△」にしておきます。

 

面積はA+Cと同じなので、7.5ｇです。△の数字は食塩水の重さなので、これを求めるには食塩の重さを濃度で割ると良かったですね。10％の食塩水（青い四角形）の重さは7.5ｇ÷0.05＝150ｇであることがわかりました。

 

ここまでくれば、5％の食塩水（赤い四角形）の横の数字もわかりますね。250ｇ-150ｇ＝100ｇです。

 

答え：5％の食塩水は100ｇ、10％の食塩水は150ｇ

SPI対策なら簡単な問題が解ければOK

SPIの食塩水の濃度の問題はそれほど難しくないようですので、基本の問題が解ければ大丈夫ではないでしょうか。裏ワザの裏ワザ、「100ｇの食塩水の濃度と食塩の重さは同じ」を使えばほとんどの問題は暗算で出来ますよ。

 

難しい問題に時間を割くよりも、簡単な問題をミスなく確実に解くことを考えて得点につなげましょう。企業側でも難しい公式を知っているかどうかより、人間性や社会性を重視しているはずです。

食塩水の公式を使った中学生の問題

今の小学生は今の大人たちが子供だった時よりも、かなり難しい勉強をしているようです。頑張って中学入試の勉強をしているお子さんを、たまにはほめてあげてくださいね。

 

ここからは中学校で習う、方程式を使った食塩水の濃度の問題をご紹介します。考え方によっては中学校で習う方法の方が簡単かもしれませんね。公式さえきちんと分かっていれば、解きやすい問題ばかりですよ。

1次方程式を使ってみよう

食塩水の濃度の問題は公式が分かっていれば、方程式を使って楽に解くことができます。ではまず一次方程式を使った、食塩水の濃度の問題を見てみましょう。

【解き方】

今までは水を蒸発させる問題は無かったですね。食塩水の濃度の問題は、食塩の重さが分かっていれば大丈夫です。まずは最初の食塩水に含まれている食塩の重さを、はっきりさせましょう。

 

最初の食塩水の食塩の量は600ｇ×0.06＝36ｇです。これが分かっていれば、あとは方程式を立てて計算するだけです。蒸発させた水の量をｘｇとして式を作りましょう。

 

600ｇの食塩水からｘｇを蒸発させたのなら、食塩の量は変わらず食塩水の量だけが減ります。出来上がった食塩水の重さは計算できますので、そこから式を作っていきます。

 

食塩水の重さの公式は食塩の重さ×濃度（小数）だったので、式は以下のようになります。

600ｇ－ｘｇ＝36ｇ×0.09

ここで注意したいのは、ｘgは蒸発させた水の量であることです。出来上がった食塩水の量は「600ｇ-ｘｇ」になりますよ。間違えやすいので気を付けましょう。あとは計算していくだけです。

600-ｘ＝36÷0.09

-ｘ＝36÷0.09-600

-ｘ＝400-600

-ｘ＝-200

ｘ＝200

 

答え：200ｇ

連立方程式の解き方

中学受験の食塩水の濃度の問題は、面積図などを使って非常にめんどうでした。同じ問題を連立方程式を使うと、どうなるかやってみましょう。

【解き方】

2つの答えを求める問題も、連立方程式を使えばらくちんですよ。濃度の問題はまず食塩の量をはっきりさせるのがポイントでしたので、8％の食塩水に含まれる食塩の重さをまず求めておきましょう。

食塩の量は食塩水の重さ×濃度（小数）だったので、250ｇ×0.08＝20ｇです。

 

次にｘとｙを決めます。5％の食塩水の重さをｘ、10％の食塩水の重さをｙとして計算式を作りましょう。出来上がった食塩水が250ｇですので、一つ目の式は

ｘ＋ｙ＝250

あとは食塩水の3つの公式のうちどれを使ってもいいのですが、食塩の重さを求める式は掛け算で計算できるので式を作りやすいですね。食塩の重さは食塩水の重さ×濃度（小数）だったので

20＝0.05ｘ＋0.1ｙ

 

あとはさっき作った式を代入して計算すればオーケーです。

ｙ＝250-ｘなので、

0.05ｘ＋0.1（250-ｘ）＝20

0.05ｘ＋25-0.1ｘ＝20

-0.05ｘ＋25＝20

-0.05ｘ＝20-25

-0.05ｘ＝-5

ｘ＝-5÷-0.05

ｘ＝100

 

先ほどの式にｘの値を代入してｙの値を求めると

ｙ＝250－100

ｙ＝150

 

答え：5％の食塩水は100ｇ、10％の食塩水は150ｇ

まとめ～食塩水の公式は3つだけ

食塩水の濃度の問題は、苦手意識のあるお子さんが多くいます。もしかしたら大人も、苦手な人が多いかもしれませんね。

たった3つの公式ですが、覚えるのは意外と面倒なのでいろいろと工夫した勉強法が編み出されているようです。

 

最近では中学受験以外にも、入社試験の適性試験にも使われるようになった食塩水の濃度の問題。基本さえ理解すれば意外と簡単に解けますので、ぜひチャレンジしてみてくださいね。